Золотое сечение в природе, человеке, искусстве
Прежде, чем мы начнем, хотелось бы уточнить ряд неточностей. Во-первых, само определение золотого сечения в данном контексте не совсем верно. Дело в том, что само понятие «сечение» – это термин геометрический, обозначающий всегда плоскость, но никак не последовательность чисел Фибоначчи.
И, во-вторых, числовой ряд и соотношение одного к другому, конечно, превратили в некий трафарет, который можно накладывать на все, что кажется подозрительным, и очень радоваться, когда есть совпадения, но все же, здравый смысл терять не стоит.
Однако, «все смешалось в нашем королевстве» и одно стало синонимом другого. Так что в общем и целом, смысл от этого не потерялся. А теперь к делу.
Вы удивитесь, но золотое сечение, точнее пропорции максимально приближенные к нему, можно увидеть практически везде, даже в зеркале. Не верите? Давайте с этого и начнем.
Пропорции золотого сечения в человеке
Знаете, когда я училась рисовать, то нам объясняли, как проще строить лицо человека, его тело и прочее. Все надо рассчитывать, относительно чего-то другого.
Все, абсолютно все пропорционально: кости, наши пальцы, ладони, расстояния на лице, расстояние вытянутых рук по отношению к телу и так далее. Но даже это не все, внутреннее строение нашего организма, даже оно, приравнивается или почти приравнивается к золотой формуле сечения. Вот какие расстояния и пропорции:
от плеч до макушки к размеру головы = 1:1.618
от пупка до макушки к отрезку от плеч до макушки = 1:1.618
от пупка до коленок и от коленок до ступней = 1:1.618
от подбородка до крайней точки верхней губы и от нее до носа = 1:1.618
Разве это не удивительно!? Гармония в чистом виде, как внутри, так и снаружи. И именно поэтому, на каком-то подсознательном что-ли уровне, некоторые люди не кажутся нам красивыми, даже если у них крепкое подтянутое тело, бархатная кожа, красивые волосы, глаза и прочее и все остальное. Но, все равно, малейшее нарушений пропорций тела, и внешность уже слегка «режет глаза».
Короче говоря, чем красивее кажется нам человек, тем ближе его пропорции к идеальным. И это, кстати, не только к человеческому телу можно отнести.
Золотое сечение в природе и ее явлениях
Классическим примером золотого сечения в природе является раковина моллюска Nautilus pompilius и аммонита. Но это далеко не все, есть еще много примеров:
в завитках человеческого уха мы можем увидеть золотую спираль;
ее же (или приближенную к ней) в спиралях, по которым закручиваются галактики;
и в молекуле ДНК;
по ряду Фибоначчи устроен центр подсолнуха, растут шишки, середина цветов, ананас и многие другие плоды.
Друзья, примеров настолько много, что я просто оставлю тут видеоролик (он чуть ниже), чтобы не перегружать текстом статью. Потому что, если эту тему копать, то можно углубиться в такие дебри: еще древние греки доказывали, что Вселенная и, вообще, все пространство, – спланировано по принципу золотого сечения.
Вы удивитесь, но эти правила можно отыскать даже в звуке. Смотрите:
Наивысшая точка звука, вызывающая боль и дискомфорт в наших ушах, равна 130 децибелам.
Делим пропорцией 130 на число золотого сечения φ = 1,62 и получаем 80 децибел — звук человеческого крика.
Продолжаем пропорционально делить и получаем, скажем так, нормальную громкость человеческой речи: 80 / φ = 50 децибел.
Ну, а последний звук, который получим благодаря формуле – приятный звук шепота = 2,618.
По данному принципу можно определить оптимально-комфортное, минимальное и максимальное число температуры, давления, влажности. Я не проверяла, и не знаю, насколько эта теория верна, но, согласитесь, звучит впечатляюще.
Главное, только не увлекаться этим, ведь если мы хотим что-то в чем-то увидеть, то увидим, даже если этого там нет
Вот я, например, обратила внимание на дизайн PS4 и увидела там золотое сечение =) Впрочем, эта консоль настолько классная, что не удивлюсь, если дизайнер, и правда, что-то там мудрил
Золотое сечение в искусстве
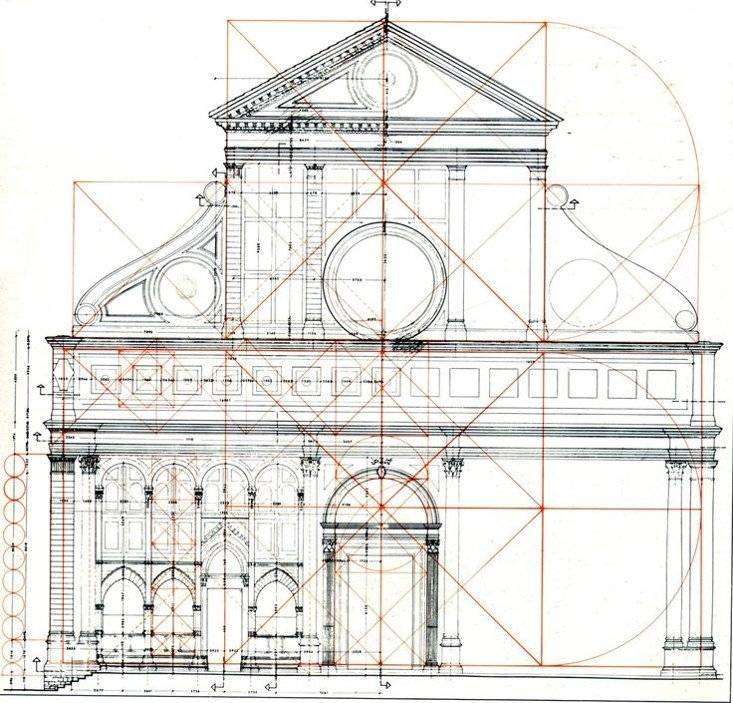
Тоже очень большая и обширная тема, которую стоит рассмотреть отдельно. Тут лишь помечу несколько базовых моментов. Самое примечательное, что многие произведения искусства и архитектурные шедевры древности (и не только) сделаны, по принципам золотого сечения.
Египетские и пирамиды Майя, Нотр-дам де Пари, греческий Парфенон и так далее.
В музыкальных произведениях Моцарта, Шопена, Шуберта, Баха и прочих.
В живописи (там это наглядно видно): все самые знаменитые картины известных художников сделаны с учетом правил золотого сечения.
Эти принципы можно встретить и в стихах Пушкина, и в бюсте красавицы Нефертити.
Даже сейчас правила золотой пропорции используются, например, в фотографии. Ну, и конечно, во всем остальном искусстве, включая кинематограф и дизайн.
https://youtube.com/watch?v=c3SVIQBXMnA
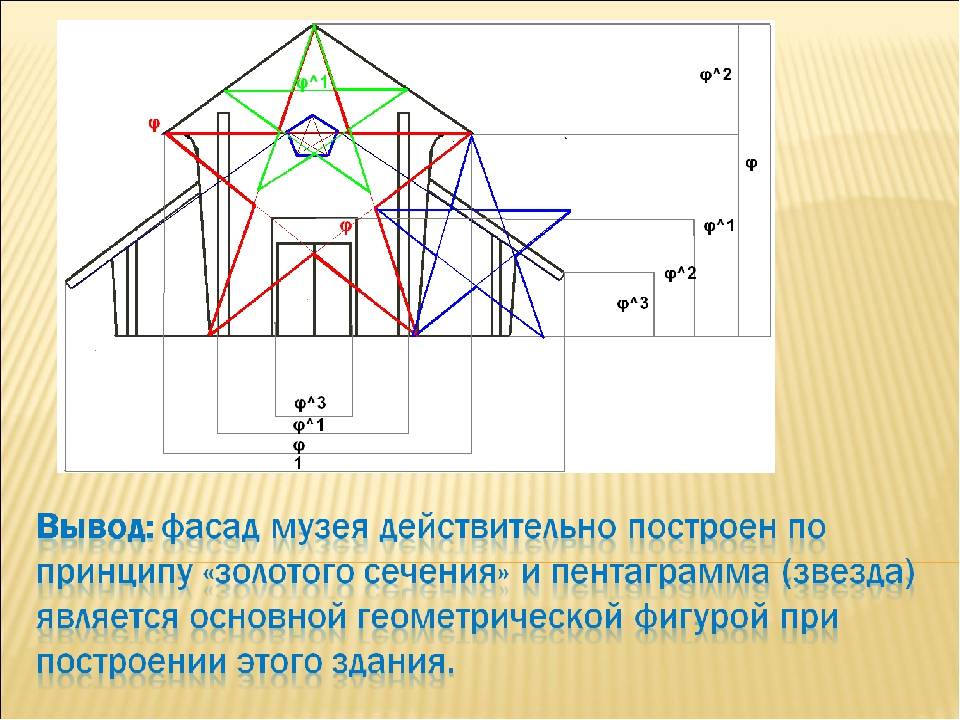
Идеальный треугольник и пентаграмма
Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.
Золотой треугольник, правило его построения и применение в создании интерьера, например
Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.
- Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
- Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.
Построение пентаграммы
- Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
- Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.
Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.
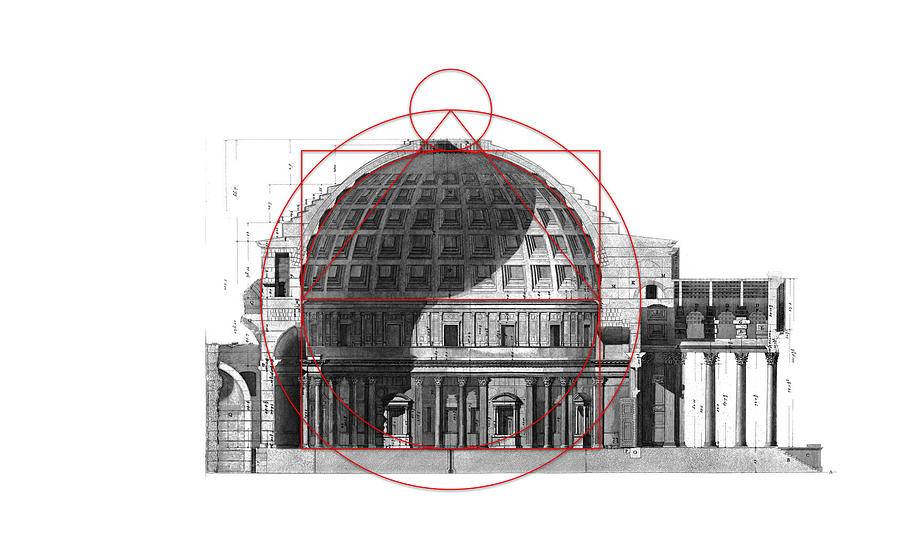
Божественная гармония золотого сечения в архитектуре: фото древних построек и примеры современного строительства
Многие древние здания, которые сохранились до наших времен, подтверждают мнение, что они были построены по правилам идеальной пропорции. Это резиденции королей, церкви, общественные сооружения. Рассмотрим на примерах принцип золотого сечения в разных странах.
Тайны древнеегипетской архитектуры
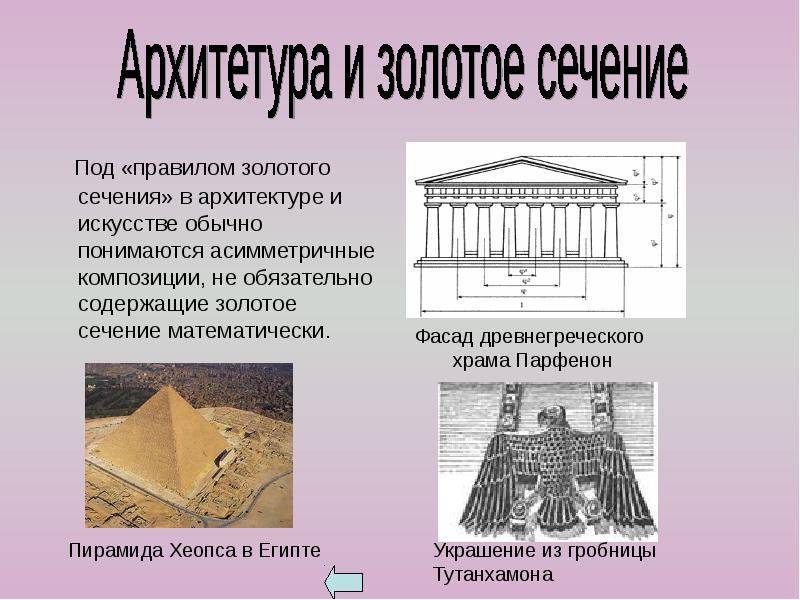
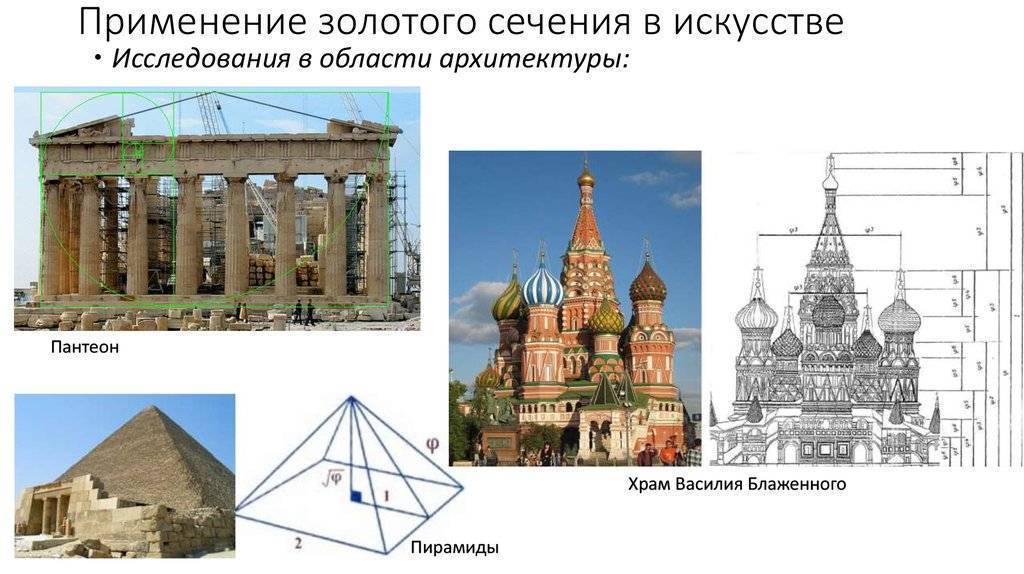
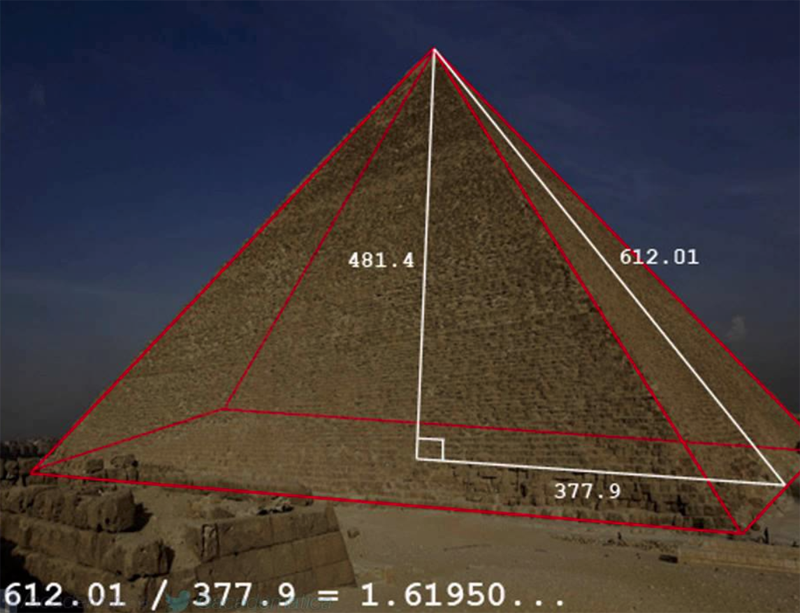
В архитектуре Древнего Египта по правилам золотой пропорции была построена пирамида Хеопса. Глядя на творение строителей, можно увидеть треугольник с прямым углом, один катет которого является высотой, второй – половиной длины основания. Если взять отношение гипотенузы к меньшей стороне, получим идеальное значение 1,61950 или 1,62.
Было замечено, что пирамида улучшает психоэмоциональное состояние человека, в её области уменьшаются вредоносные излучения, пропадают геопатогенные зоны.Идеальная пропорция золотого сечения в пирамиде
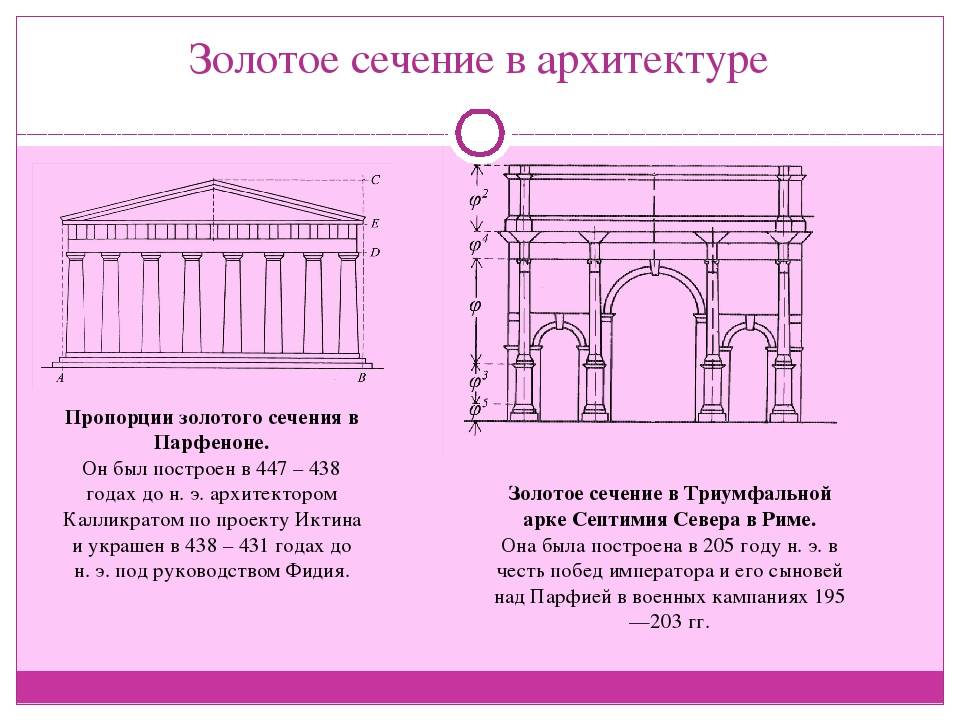
Идеальные пропорции в древней Греции
Идеальная пропорциональность делает архитектурные объекты запоминающимися. Яркий представитель ЗС из древней Греции – Парфенон, который возведен в 5 веке до нашей эры. Если взять отношение его высоты к ширине, получится практически идеальное число 0,618.
Ученые определили, что для абсолютного золотого числа нужно отнять от высоты 14 см и прибавить их к ширине. Учитывая строение сооружения, очень похоже, что это было сделано древними архитекторами Иктином и Калликратом намеренно, поскольку фасад немного сужается в верхней части и отклоняется от золотого прямоугольника. Но общие пропорции ЗС соблюдены.
Памятники архитектуры средневековья
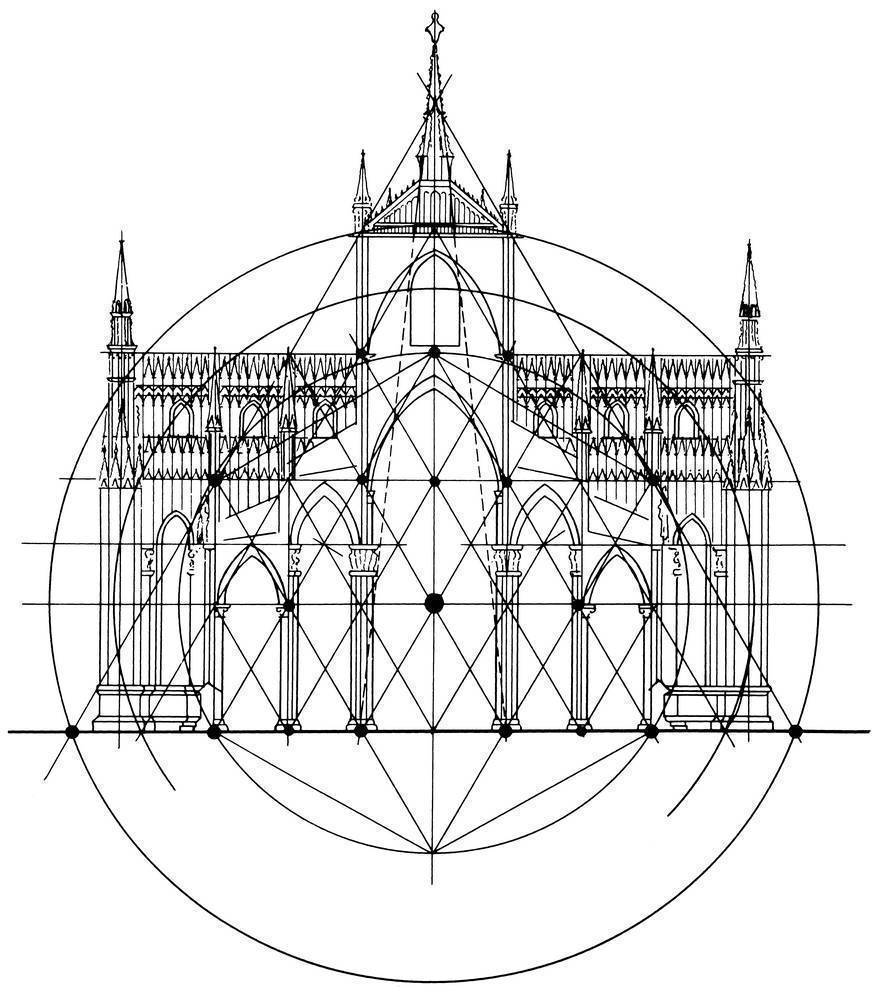
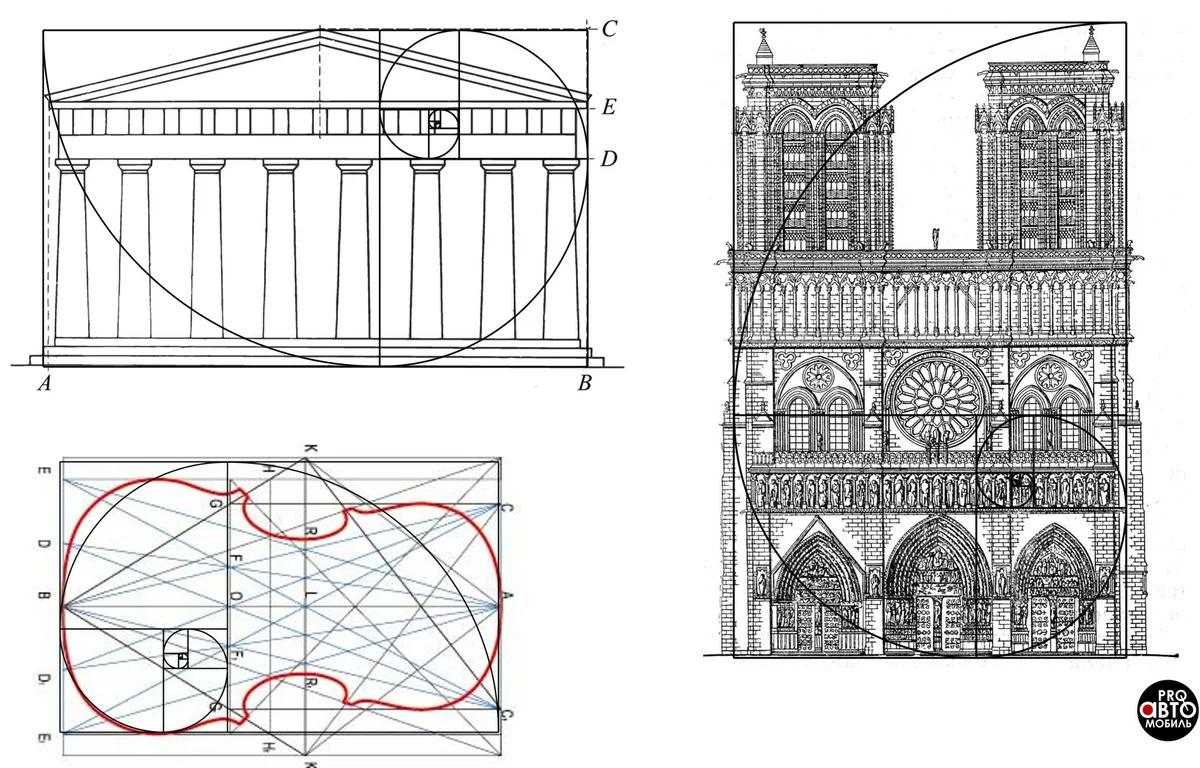
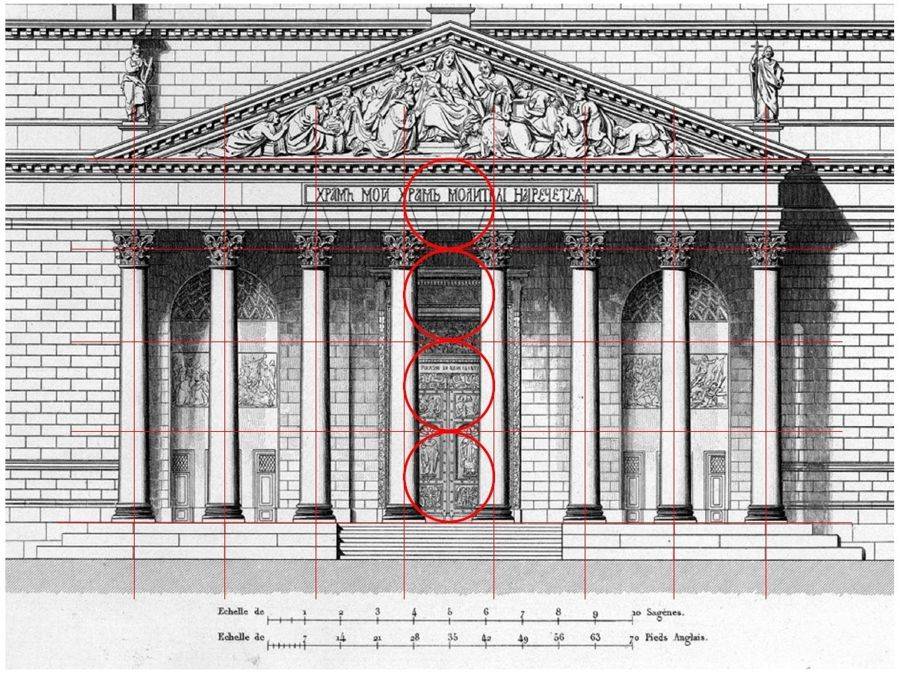
Прекрасным памятником истории архитектуры средневековья, сохранившимся до нашего времени, является собор Парижской Богоматери или Нотр-Дам де Пари.
В здании очень заметно желание архитектора соблюсти гармонию и целостностьАнализируя строение, принцип ЗС можно видеть на нескольких участках
Математические и эстетические свойства
(Рис.2) Построение золотого прямоугольника
Обычно названия золотого сечения (отношения), часто встречается как золотое сечение (латинский: sectio aurea) и золотая середина .,, Другие описания, с которыми часто сталкиваются, применяют выражения как необычное или как среднее сечение , как божественная пропорция, что на (латинском: sectio divina); также как золотая пропорция, золотое сокращение, золотое число, а также как среднее из Phidias.,,Золотое сечение часто обозначается греческой буквой — .
Фигура (см. Рис.2) иллюстрирует геометрические отношения, которые определяют эту константу:
По крайней мере со времён Ренессанса, много художников и архитекторов строили свои работы так, чтобы приблизить золотое сечение (отношение) к правилам золотого прямоугольника, в котором отношение более длинной стороны к корткой было золотым отношением, равной золотой пропорции, удовлетворящее эстетические восприятия.
Алгебраически нахождение золотого сечения (см. Рис.2) отрезка длины сводится к решению уравнения:
- , где = 1.6180339887 (для сравнения (см. Рис.1) ),
откуда:
Отношение может быть также выражено приближенно дробями
где — числа Фибоначчи.
Иррациональное алгебраическое число
Отношение частей в этой пропорции выражается квадратичной иррациональностью
(Греческая буква «фи», первая буква имени Фидиас (Phidias), введённая для обозначения золотого сечения) — иррациональное алгебраическое число, положительное решение квадратного уравнения
представляется в виде бесконечной цепочки квадратных корней:
представляется в виде бесконечной цепной дроби
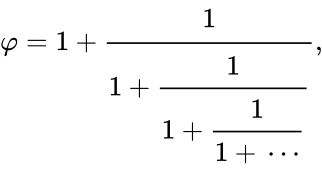
- подходящими дробями которой служат отношения последовательных чисел Фибоначчи . Таким образом, .
Золотое сечение в пятиконечной звезде
Построение золотого сечения
В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 до н. э.), где оно применяется для построения правильного пятиугольника.
- В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении (на приведённом рисунке отношение красного отрезка к зелёному, так же как зелёного к синему, так же как синего к фиолетовому, равны ).
- Геометрическое построение. Золотое сечение отрезка можно построить следующим образом: в точке восстанавливают перпендикуляр к , откладывают на нём отрезок , равный половине , на отрезке откладывают отрезок , равный , и наконец, на отрезке откладывают отрезок , равный . Тогда
Золотое сечение в психологии
Числа Фибоначчи и золотое сечение также используются в психологии. Например, чтобы выяснить, как складывается механизм творчества, В.В. Клименко использовал математику, а именно законы чисел Фибоначчи и соотношение «золотого сечения», законы природы и жизни человека. Если разложить числа Фибоначчи в ряд, то получится: 1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и т д. Отношение чисел Фибоначчи равно 0,618. Развитие человека также происходит по этому соотношению и подчиняется закону своих чисел, разделяя жизнь на этапы с определенными доминантами механизма творчества.
Числа Фибоначчи делят человеческую жизнь на этапы по количеству прожитых лет:
0 — начало отсчета (ребенок родился). Ему еще не хватает не только психомоторики, мышления, чувств, воображения, но и оперативного энергетического потенциала. Он — начало новой жизни, гармонии.
1 — ребенок начинает ходить и осваивать окружающее пространство.
2 — кроха понимает речь и действует, используя словесные указания.
3 — малыш действует через слово, задает вопросы.
5 — «возраст грации». Наблюдается гармония психомоторики, памяти, воображения и чувств, которые уже позволяют ребенку охватить мир во всей его полноте.
8 — Чувства выходят наружу. Им служит воображение, а мышление силами своей критичности направляется на поддержание внутренней и внешней гармонии…
Видео описание
В этом видео представлен пример применения принципа золотого сечения в обстановке дома:
Выбор цвета по правилам золотого сечения
Обычно при выборе цветовой гаммы пользуются соотношением 10-30-60, которое основывается на золотом сечении.
Таким образом, пространство должно состоять из трёх цветов: первый – доминирующий, который будет охватывать 60% комнаты, этот цвет припадает на стены и пол.
За ним следует второй, который составляет 30% – это мебель. И третий, составляющий 10%, используется для небольших предметов, тот же декор.
Подвесной декор
Разделите свободную площадь стены на три равные части по горизонтали и вертикали, прямоугольник, который окажется внутри и будет привлекать основное внимание гостей.
Золотое сечение в мебели
Необходимое число и нужные размеры мебели определяют, отталкиваясь от габаритов самых крупных ее представителей – шкафов, диванов, столов, и т. д. Например, если шкаф-стенка занимает две трети от всей площади комнаты, тогда диван-кровать должен быть в пределах 2/3 от величины шкафа. По тому же принципу строится соотношение размеров стола к дивану, кресел к столу, стульев к креслам и т.д.
То же самое и с декором, большие предметы комбинируются с более мелкими, с сохранением соотношения золотой пропорции.
Есть фирмы, которые выпускают целые наборы мебели, спроектированные, с уже правильным соотношением размеров отдельных элементов набора.
Принцип расчета и построения золотого сечения
Примеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений, только нужно знать, как правильно его увидеть. Для этого достаточно посмотреть на строение всего 5 минут.
Как определить число золотого сечения
С пропорцией ЗС связывают астронома из Италии Фибоначчи, он вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Сегодня эта закономерность известна как ряд Фибоначчи:
- 0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и так до бесконечности;
- если выполнить деление последующего числа на предыдущее – получится коэффициент ЗС.
Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленные значения 0,62 и 0,38.
Ряд Фибоначчи в церкви Покрова на Нерли
Как рассчитать золотое сечение на простейшем примере
Проще всего объяснить гармонию ЗС можно на примере обычного куриного яйца, точнее на удалении всех точек скорлупы от центра тяжести. Именно форма оболочки, а не её прочность, обеспечила выживаемость птиц столь долгое время и в любых условиях.
Если взять обычный отрезок, который состоит из нескольких маленьких, их длины относятся к большей величине как 0,62. Это показывает, как можно разбить целую линию для получения идеальной пропорции.
Простой пример золотого сечения в курином яйце
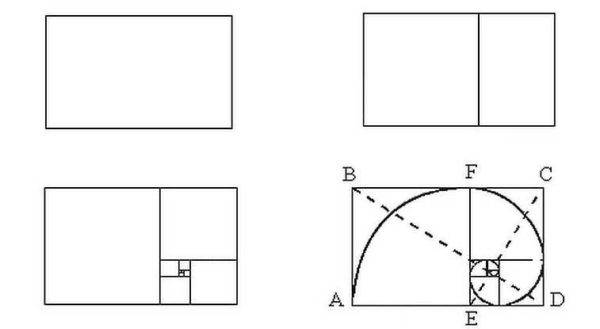
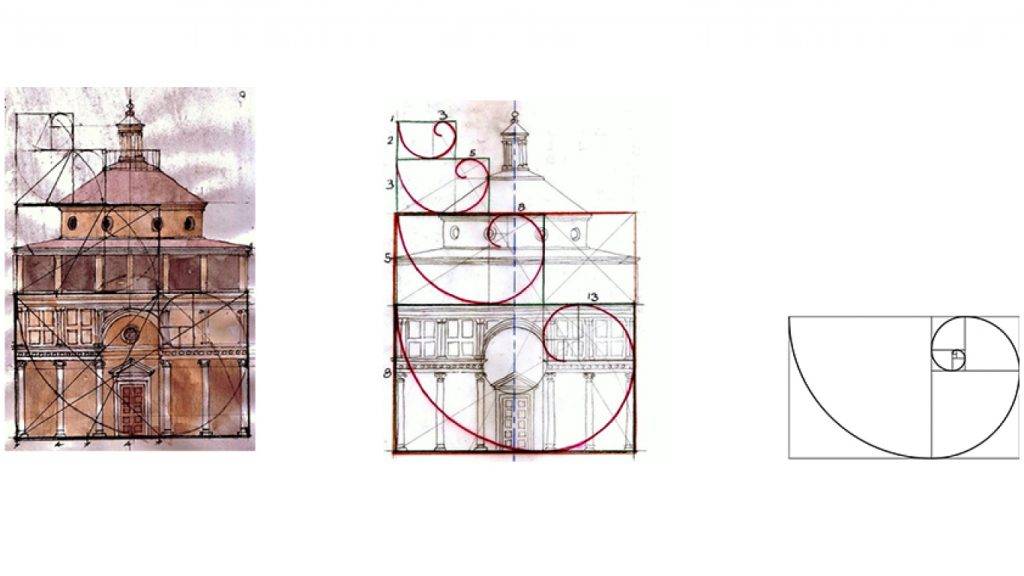
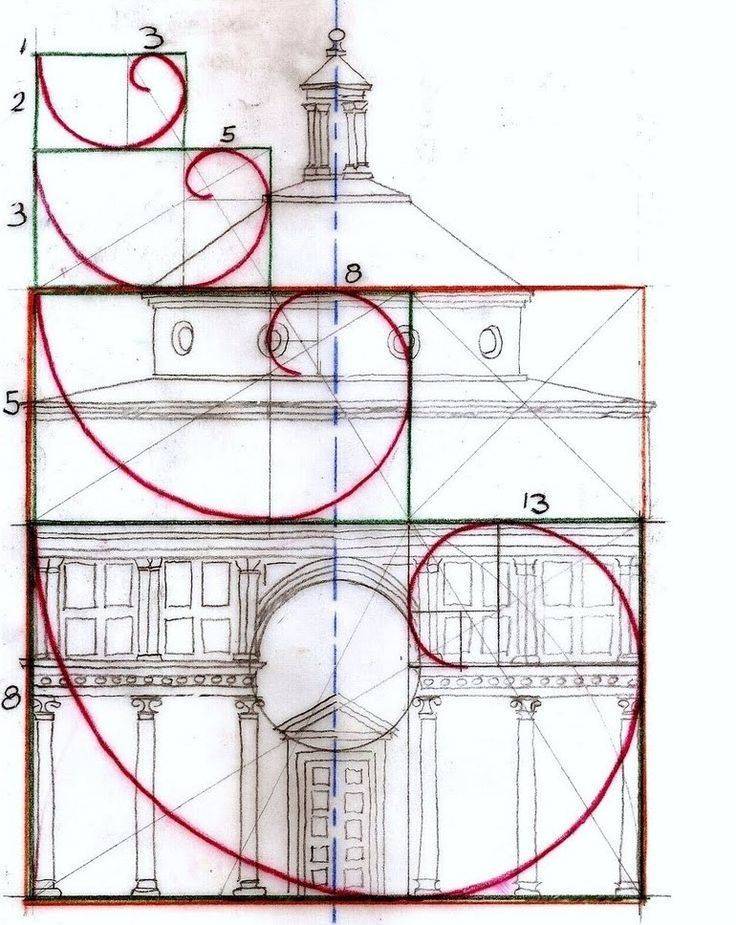
Как построить золотое сечение на примере прямоугольника и спирали
Если построить золотой прямоугольник, используя ряд Фибоначчи, он будет выглядеть как единое целое. Рассмотрим зависимость на примере:
- нужно нарисовать квадрат со стороной 1 и рядом ещё один аналогичный;
- над ними разместить квадрат со стороной 2;
- слева гармонично помещается квадрат с гранью 3;
- ниже – квадрат со стороной 5;
- справа пространство займет квадрат с гранью 8;
- площадь прямоугольника 8×13, в котором 13 — это следующее число ряда;
- если разделить на калькуляторе следующее число на предыдущее, получится значение золотого сечения 1,62, причём, чем больше числа, тем меньшая погрешность в их отношении;
- если по этому принципу построить спираль, каждую четверть витка она будет расширяться именно на значение ЗС.Принцип золотого сечения в прямоугольникеПостроение золотой спирали из прямоугольника
Божественная гармония золотого сечения в архитектуре: фото древних построек и примеры современного строительства
Многие древние здания, которые сохранились до наших времен, подтверждают мнение, что они были построены по правилам идеальной пропорции. Это резиденции королей, церкви, общественные сооружения. Рассмотрим на примерах принцип золотого сечения в разных странах.
Тайны древнеегипетской архитектуры
В архитектуре Древнего Египта по правилам золотой пропорции была построена пирамида Хеопса. Глядя на творение строителей, можно увидеть треугольник с прямым углом, один катет которого является высотой, второй – половиной длины основания. Если взять отношение гипотенузы к меньшей стороне, получим идеальное значение 1,61950 или 1,62.
Было замечено, что пирамида улучшает психоэмоциональное состояние человека, в её области уменьшаются вредоносные излучения, пропадают геопатогенные зоны.
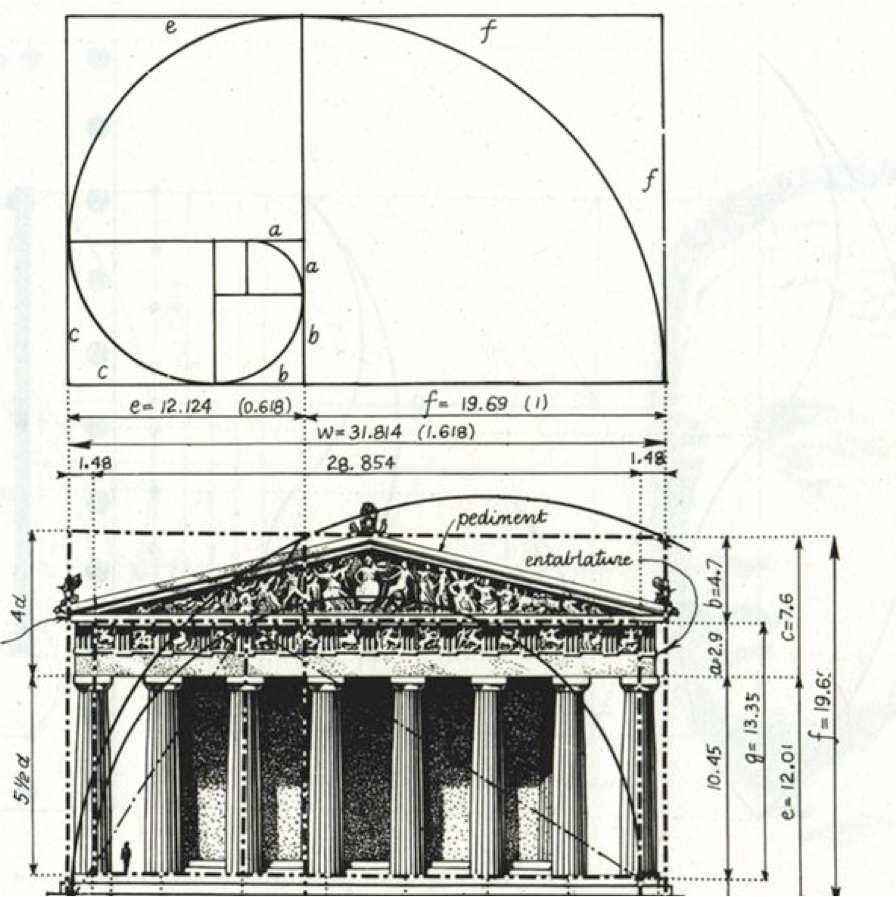
Идеальные пропорции в древней Греции
Идеальная пропорциональность делает архитектурные объекты запоминающимися. Яркий представитель ЗС из древней Греции – Парфенон, который возведен в 5 веке до нашей эры. Если взять отношение его высоты к ширине, получится практически идеальное число 0,618.
Ученые определили, что для абсолютного золотого числа нужно отнять от высоты 14 см и прибавить их к ширине. Учитывая строение сооружения, очень похоже, что это было сделано древними архитекторами Иктином и Калликратом намеренно, поскольку фасад немного сужается в верхней части и отклоняется от золотого прямоугольника. Но общие пропорции ЗС соблюдены.
Принцип идеальной пропорции в древнегреческом Парфеноне:


Памятники архитектуры средневековья
Прекрасным памятником истории архитектуры средневековья, сохранившимся до нашего времени, является собор Парижской Богоматери или Нотр-Дам де Пари.

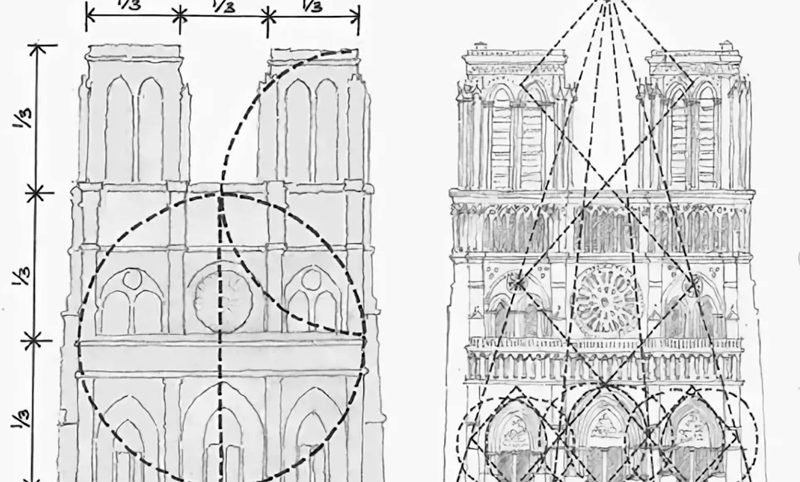
Архитектура России
Ряд Фибоначчи – это своеобразная матрица, с помощью которой анализируют любое архитектурное сооружение. Чтобы было проще ориентироваться, можно построить на принципе золотого сечения циркуль Фибоначчи.



Золотое сечение в архитектуре Москвы
Выдающееся здание МГУ на Воробьевых горах было построено в послевоенное время. В те годы это было самое высокое строение, состоящее из пяти композиционных групп, которые венчает центральная башня. Здесь чётко прослеживается треугольник с прямым углом, гипотенуза которого захватывает пристройки и проходит через угол здания.

Золотые пропорции прослеживаются и в работах русского зодчего Матвея Казакова.




Использовал это прием и архитектор Василий Баженов, его здания причислены к историческим памятникам

Архитектура в Санкт-Петербурге
Живым примером золотого сечения является Исаакиевский собор.
В первую очередь можно проанализировать его ширину, равную 400 единицам:
- при делении числа 400 на значение золотого сечения получим приблизительно 248;
- при дальнейшем делении 248/1,618=153;
- основная часть собора вписывается в золотой прямоугольник, длинная сторона которого равна 400, ширина – 248.
По высоте здания ЗС можно видеть у купола, благодаря этому внешнее восприятие памятника архитектуры становится гармоничным.

Приведем ещё несколько примеров золотого сечения в архитектуре Санкт-Петербурга.
Кунсткамера
Кунсткамера была построена ещё в 1718 году, руководил строительством немецкий архитектор Георг Маттарнови. Она представляет собой 2 корпуса по 3 этажа, между ними возведена куполообразная многоярусная конструкция в виде башни.Золотое сечение в соотношении сторон можно наблюдать в длине корпусов и в высотах разных уровней.
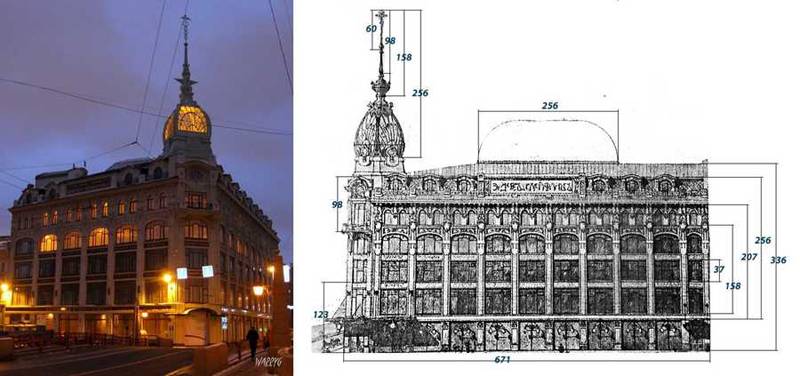
Торговый дом Эсдерс и Схейфальс
ЗС в здании, возведенном в 1907 году, наблюдается в следующих размерах:
671, 414, 256, 98, 60, 37 и 23.
Композиция смотрится гармонично благодаря золотому соблюдению высотных величин.
Дом Советов
Дом Советов был возведен по проекту Троцкого в 1941 году, основной акцент выполняют портик по центру с 14 колоннами и скульптурный ансамбль. По обе стороны расположены два корпуса высотой в 5 этажей. Длина здания – 1472 единицы, если разделить его на значение Ф = 1,618, получим размерный ряд:
1472, 909, 562, 347, 214, 132, 81, 50. К ним относятся высота входа, всего сооружения, различных элементов.
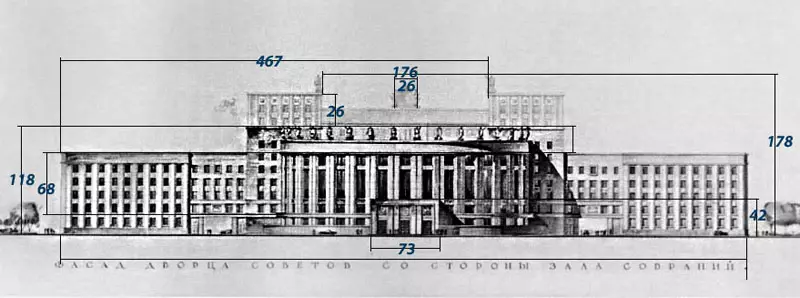
Золотой прямоугольный треугольник идеально вписывается в центр здания, его вершина совпадает с вершиной Дома Советов, а гипотенуза заканчивается в конце бокового крыла. Если построить равнобедренный золотой треугольник, его грани будут проходить через точки в верхней части основного входа.

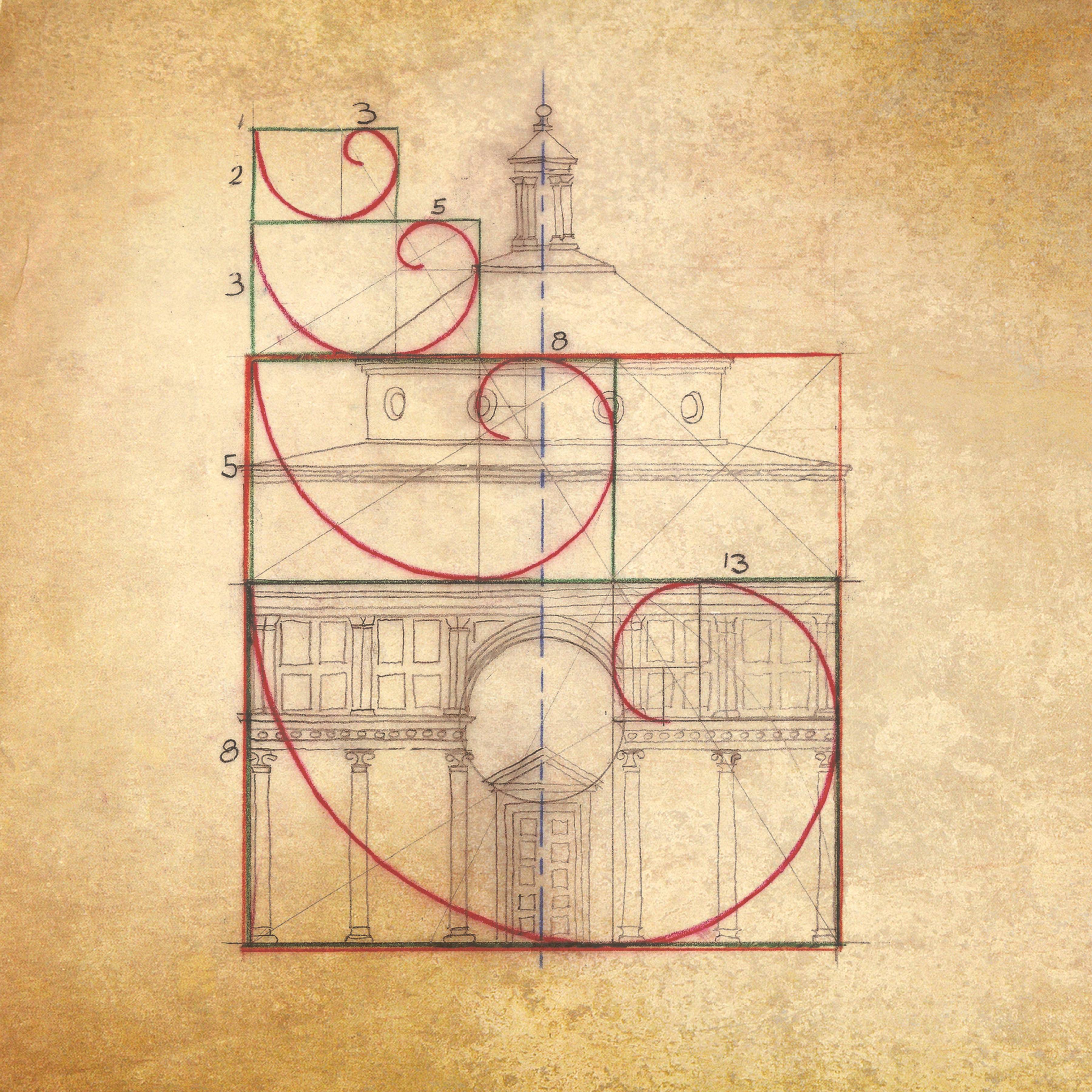
Примеры золотого сечения в современной архитектуре
В современной архитектуре формула расчёта золотого сечения позволяет проектировать уникальные формы, которые несут прочность, спокойствие и красоту.




Использование золотых пропорций в интерьере вашего дома, квартиры
При взгляде на красиво обустроенный домашний интерьер, первое, что бросается в глаза – это легкая асимметрия, едва уловимый беспорядок. Помещение, оформленное в соответствии с золотыми пропорциями, дает ощущение спокойствия, умиротворенности. В идеальном по форме помещении соотношение ширины к длине будет 5 к 8, или 1 к 1,62.
В начале 20 века, для планирования приемлемых жилых пространств человека, архитектор Ле Корбюзье придумал систему антропометрических пропорций, названную «модулор». Она представляет собой стилизованную фигурку человека с поднятой рукой. Рост, пропорции взяты идеальные, усредненные, изначально они использовались в строительстве первых многоквартирных домов.
При планировке пространства
На стадии расчетов рисуется планировка, которая разбивается на части по принципу «золотой» спирали. Зонирование пространства, особенно большого, производится в четком соответствии с точками пересечения основных линий – здесь расставляется мебель, ширмы, экраны или перегородки в квартире-студии
Основные акценты, на которые хочется обратить внимание, также размещают в данных точках
Когда в доме много помещений, их также можно идеально распланировать: тогда самая большая комната станет относиться к площади всей квартиры как 0,62 к 1, меньшая – точно также к площади большей, кухня – к меньшей комнате, прихожая к кухне, санузел к прихожей, балкон – к санузлу.
Золотое сечение в соотношении размеров
Желательно, чтобы диван не занимал больше, чем две трети стены, около которой он стоит, а журнальный столик – максимум две трети размера дивана. Высота прикроватных тумбочек, с расположенными на них лампами, выбирается высотой 2/3 стены.
Большие темные предметы размещают снизу, маленькие, более светлые – выше, чтобы создавалось своеобразное ощущение покоя. Любые длинные отрезки, направленные сверху вниз, создают давящее впечатление, восходящие – наоборот. Картины разного размера следует тщательно подбирать по отношению друг к другу, развешивать на соответствующей высоте.
Золотое сечение в цветовой гамме
Весьма гармонично смотрится помещение, где 62-65% всего пространства уделяется основному цвету, остальные 35-38% — второстепенному, до 5% — разнообразным цветовым акцентам. Оклейка стен обоями разного цвета, но схожей фактуры, осуществляется по такому же принципу.
Золотое сечение при выборе высот
Высота прикроватных тумбочек, с расположенными на них лампами, выбирается в размере 2/3 стены. Если выбрана облицовка стен пластиковыми, деревянными панелями, керамической плиткой, то она также займет две трети высоты – остальное пойдет под покраску, оклейку обоями. Примерно одну треть высоты шкафов займут диваны со спинками, кухонные столешницы, а низенькие «восточные» столики – треть их высоты.
Нижние точки любых потолочных светильников не опускают ниже, чем на пять восьмых высоты комнаты. Если данную пропорцию соблюсти не удается, то расположение светильников «привязывают» к другим предметам интерьера. Стоящие рядом друг с другом однотипные элементы декора также должны соотноситься друг с другом как 1 к 1,62.
Золотое сечение в мебели, декоре
При расстановке меблировки следует учитывать, что ею занимают не более 65% площади комнаты – иначе комната будет выглядеть тесной. Идеальное количество, габариты мебели рассчитывают, исходя из размеров самых крупных ее предметов – шкафа, дивана, большого стола, кухонного гарнитура. Например, шкаф-стенка займет две трети всего помещения, тогда диван-кровать выйдет 2/3 размера шкафа. Таким же образом стол будет относиться к дивану, кресла к столу, стулья к креслам и др. Крупные элементы декора дублируются на разных местах пространства такими же более мелкими, но с соблюдением пропорций.
5 способов соблюдать правило в интерьере
- В доме, построенном без учёта соотношения, можно сделать перепланировку комнат, чтобы пропорции соответствовали.
- Иногда достаточно переставить мебель или сделать дополнительную перегородку.
- Аналогичным образом меняется высота и длина окон и дверей.
- В цветовом оформлении получение упрощённого соотношения достигается за счёт 60% основного цвета, 30% — оттеняющего, и остальных 10% — усиливающих восприятие тонов.
- Высота и длина мебели должна соизмеряться высотой потолков и шириной простенков.
Приложение этой нормы в интерьере, как архитектурно оформленном пространстве, объединяют с понятиями самоорганизации, рекурсии, асимметрии, красоты.
Как построить прямоугольник с идеальными пропорциями
Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.
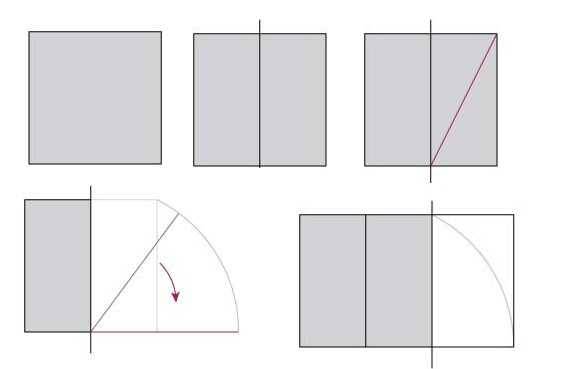 Построение прямоугольника с золотым сечением
Построение прямоугольника с золотым сечением
Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы. Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).
 Это явно неспроста. Хотя далеко не все подчиняется этой закономерности
Это явно неспроста. Хотя далеко не все подчиняется этой закономерности
Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.
Как использовать пропорциональность в интерьере
Возникает вопрос- а что дает на практике знание закона золотого сечения и гармоничной пропорции. Вот некоторые приемы, использующие эти знания.
Например, для отделки стен мы хотим использовать деревянные панели. При этом будем обшивать стену не на всю высоту, а частично. Чтобы панели смотрелись гармонично, можно использовать два варианта обшивки стены.
- Вначале замеряйте высоту стены и умножьте её значение на 0,618 ( «золотое число»).
- Запишите полученное значение.
- Теперь из общей высоты стены вычтите его..
- В результате мы имеем два значения высот для обшивки панелями стены.
- Первое = высота стены умноженная на 0,618, а второе равно высота стены минус высота, умноженная на 0,618.
Этот же прием можно использовать и при оклеивании стен обоями. Разделив стену по высоте на бордюр,фриз и основное полотно обоев.
Пропорциональность можно использовать при зонировании пространства. Для этого можно разбить стену вертикалью на части по правилу золотого сечения и отделывать полученные сегменты стены разными материалами или разным цветом.
.Пропорциональность можно использовать при выборе мебели в интерьер.
например высота шкафа и стоящего рядом рядом дивана будут смотреться гармонично если соотношение их размеров будут приближены к «магическому числу» 0,618. То есть высота дивана должна быть приблизительно равна высоте шкафа умноженной на 0,618
По пропорции можно подбирать размер декоративных элементов на плоскости. Например панно или гобелен на стене или ковер на полу.
Ну и так далее, проявляйте творчество и все получится!
Кроме этого приема композиции в интерьере, вы можете ознакомиться с видеосюжетом Правила Дизайна Баланс и Порядок в котором автор рассказывает о многих композиционных приемах, применяемых в современном дизайне интерьера
Как получили золотое сечение
Пропорцию золотого сечения проще всего представить, как отношение двух частей одного объекта разной длины, разделенных точкой.
Проще говоря, сколько длин маленького отрезка поместится внутри большого, или отношение самой большей из частей ко всей длине линейного объекта. В первом случае соотношение золотого сечения составляет 0,63, во втором варианте соотношение сторон равняется 1,618034.
На практике золотое сечение представляет собой всего лишь пропорцию, соотношение отрезков определенной длины, сторон прямоугольника или других геометрических форм, родственных или сопряженных размерных характеристик реальных объектов.
Первоначально золотые пропорции были выведены эмпирическим путем с помощью геометрических построений. Существует несколько способов построения или выведения гармонической пропорции:
- Классическим разбиением одной из сторон прямоугольного треугольника и построением перпендикуляров и секущих дуг. Для этого из одного конца отрезка необходимо восстановить перпендикуляр высотой в ½ его длины и построить прямоугольный треугольник, как на схеме.
Если на гипотенузе отложить высоту перпендикуляра, то радиусом, равным оставшемуся отрезку, основание рассекается на два отрезка с длинами, пропорциональными золотому сечению;
- Методом построения пентаграммы Дюрера, гениального немецкого графика и геометра. Сегодня мы знаем метод золотого сечения Дюрера, как способ построения звезды или пентаграммы, вписанной в окружность, в которой как минимум четыре отрезка гармоничной пропорции;
- В архитектуре и строительстве золотое сечение чаще используется в усовершенствованном виде. В этом случае используется разбиение прямоугольного треугольника не по катету, а по гипотенузе, как схеме.
К сведению! В отличие от классического золотого соотношения, архитектурная версия подразумевает соотношение сторон отрезка в пропорции 44:56.
Если стандартный вариант золотого сечения для живых существ, живописи, графики, скульптур и античных построек рассчитывался, как 37:63, то золотое сечение в архитектуре с конца XVII века все чаще стало использоваться 44:56. Большинство специалистов считают изменение в пользу более «квадратных» пропорций распространением высотного строительства.
Золотое соотношение во внутреннем оформлении
Что еще дает золотое сечение кроме визуального наслаждения? Психологи говорят, что в интерьере, созданном по этому правилу человек чувствует себя более комфортно. Это, конечно, субъективно, но можно попробовать. Итак, вот как интерпретируют правило золотого сечения в дизайне интерьеров:
- Если вы собираетесь разделить комнату на зоны, воспользуйтесь правилом. Это значит, что одна из частей должна быть около 62%, вторая — 38%.
- Площадь, занятая предметами мебели, не должна быть больше чем 2/3.
- При подборе мебели руководствуемся правилом: каждый средний предмет по габаритам относится к крупным так же, как маленький к средним.
- При выборе цвета придерживайтесь примерно тех же правил:
- При использовании горизонтального деления стены (панели), высоту панели можно брать 1/3 или 2/3 от общей высоты комнаты. Но при этом мебель подбирается пропорциональной по высоте, а не по длине.
Относительно мебели правило кажется непонятным, но это только на первый взгляд. Например, подбираем группу отдыха. Крупный предмет в этом случае — диван или софа. Средний — журнальный или кофейный столик, кресла. Мелкие — аксессуары. Так вот, размеры журнального столика не должны быть больше длинной стороны дивана, кресла — не больше его короткой стороны. Аксессуары по размерам не больше размеров столика или кресел. В идеале, они соотносятся с ними как 62% и 38%.
 Пропорциональность — важная вещь
Пропорциональность — важная вещь
Почему не указывается точное соотношение? Потому что, во-первых, найти такие предметы нереально. Во-вторых, золотое сечение — это не только 62% и 38%. Это еще и последовательность Фибоначчи, следование которой также делает оформление гармоничным. Есть люди, у которых следование этой последовательности является «встроенной функцией». Им не надо считать, они выбирают основываясь на чутье и интуиции. Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.







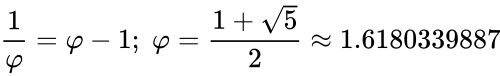
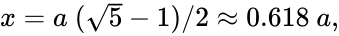
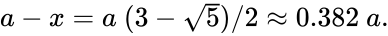
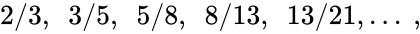
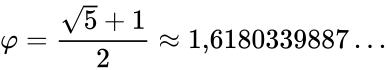
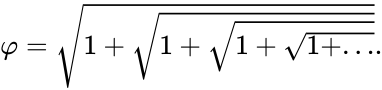
![Золотое сечение [love soft]](https://stalnoy-dekor.ru/wp-content/uploads/6/7/1/671a2e2471a71800eaecf8dcda3a0f41.jpeg)